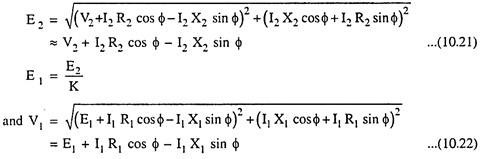Consider a transformer shown in Fig. 10.13 having primary and secondary windings of resistances R1 and R2 and reactance X1 and X2 respectively. The impedance of primary winding is given by Z1 = R1 + j X1 and impedance of secondary winding is given by Z2 = R2 + jX2.
The phasor diagrams of above transformer on:
(i) Pure resistive,
ADVERTISEMENTS:
(ii) Resistive-inductive, and
(iii) Resistive-capacitive loads are shown in Fig. 10.14(a), (b) and (c) respectively.
Draw OA representing secondary terminal voltage V2 and OI2 representing secondary current I2 in phase as well as magnitude. Since voltage drops due to secondary winding resistance and reactance are I2 R2 in phase with current I2 and I2 X2 leading current I2 by π/2 respectively, so draw AB parallel to OI2 and equal to I2 R2 in magnitude representing resistive drop in secondary winding and draw BC perpendicular to AB and equal to I2 X2 in magnitude representing reactive drop of secondary winding. Since phasor sum of terminal voltage V2, secondary resistive drop I2 R2 and secondary reactive drop I2 X2 is equal to induced emf E2 in secondary winding so phasor OC represents secondary induced emf E2.
ADVERTISEMENTS:
Hence we have:
E2 = v2 + I2 (R2 + j X2) = V2 + I2 Z2 … (10.15)
The induced emf E1 in primary winding is in phase with E2 and equal to N1/N2 E2 in magnitude, so take OD = N1/N2 OC representing E1. Produce DO to D’ taking OD’ = OD hence representing (-E1).
The induced primary current I’1 is equal to – I2 N2/N1so draw OI’1, equal to OI2 × N2/N1 by producing line I2 O. Draw line OI0 representing no-load current in magnitude as well as in phase. The phasor sum of induced primary current I’1 and no-load current I0 gives primary current represented by phasor OI1, in Fig. 10.14.
ADVERTISEMENTS:
Since voltage drop due to primary winding resistance and reactance are I1 R1 in phase with primary current I1 and I1 X1 leading current I1 by π/2 respectively, so draw D’ F parallel to OI1, and equal to I1 R1 in magnitude representing resistive drop in primary winding and draw FG perpendicular to D’ F equal to I1 X1 in magnitude representing reactive drop in primary winding. As the phasor sum of (- E1), primary resistive drop and primary reactive drop gives the applied voltage V1 to primary winding, hence phasor OG represents the applied voltage V1 in magnitude as well as in phase.
i.e. V1 = – E1 + I1 (R1 + j X1) = – E1 + I1 Z1 … (10.16)
The phase angle φ1 between V1 and I1 gives the power factor angle of the transformer.
Since no-load current I0, resistive drops I1 R1 and I2 R2 and reactive drops, I1 X1 and I2 X2 are very small, so neglecting these we have φ2 = φ’1 = φ1 = φ, the phase angle of the load. In Fig. no-load current, resistive drops and reactive drops are shown, for clarity, on exaggerated scales.
ADVERTISEMENTS:
From phasor diagrams we have:
(a) For pure resistive load [phasor diagram 10.14 (a)]
(b) For resistive-inductive load [phasor diagram 10.14 (b)]
(c) For resistive-capacitive load [phasor diagram 110.14 (c)]