In this article we will discuss about the principles of joining processes. The principles are:- 1. Soldering and Brazing and 2. Adhesive Bonding. The processes, namely, brazing, soldering, and adhesive bonding are grouped under solid / liquid state welding. The physical phenomena associated with each of these processes are essentially the same, and differ mainly in the metallurgical aspects. In these processes, the bulk material is not melted. Also, a molten filler material is used to provide the joint.
Principle # 1. Soldering and Brazing:
The soldering and brazing processes are carried out by allowing a molten filler material to flow in the gap between the parent bodies. Obviously, the filler material has to have a melting point much lower than that of the parent bodies. When the filler material is a copper alloy (e.g., copper-zinc and copper-silver), the process is called brazing. A similar process with a lead-tin alloy as the filler material is called soldering. The most common heat source for these processes is electrical resistance heating.
The copper-silver phase diagram is shown in Fig. 5.18. Here, we see that by varying the composition of the alloy the flow temperature can be controlled in the range 750-980°C. Similarly, the lead-tin phase diagram (Fig. 5.19) indicates a flow temperature in the range 160-300°C.
Two distinct advantages of this class of joining processes are obvious. First, the heating of the parent materials is negligible to cause any change in their structure or properties. Second, these processes can join two materials which are insoluble in each other.
ADVERTISEMENTS:
To produce a perfect joint, the entire gap between the parent bodies must be filled up by the filler material. This is achieved essentially through a capillary action. Thus, the spreading and the wetting capacities of the filler liquid play a predominant role towards producing a satisfactory joint. In some cases, these properties even dictate the composition of the alloy to be used. In what follows, we shall briefly discuss the adhesion between a liquid and a solid surface.
The work of adhesion between a liquid and a solid is governed by the surface free energy according to the relation –
Where V0 represents a saturated vapour. Thus, for a good wetting, γs/v should be large. This explains the difficulty of soldering or brazing grey cast iron whose surface is contaminated with graphite having a very low surface energy.
The theory of capillary flow tells us two important facts, namely:
(i) The liquid drop rises to a greater height with a reduced gap, and
(ii) The rate of rise is slower with a reduced gap.
ADVERTISEMENTS:
In fact, the optimum gap maintained, between the parts to be joined, is of the order of 0.1 mm.
The strength of a typically brazed joint varies with the thickness of the joint in a manner shown in Fig. 5.21. Here, we note that an optimum joint thickness (t0) exists at which the strength is maximum. For a very large thickness of the joint, the strength of the joint approaches that of the brazing alloy (σfiller). Below the optimum thickness, the entire joint is not filled up due to the strong resistance against the capillary flow. Hence, the strength is low due to the lack of a perfect fit.
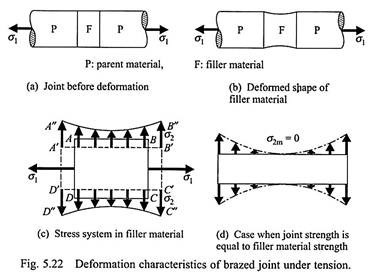
It can be seen that the maximum joint strength is higher than the strength of the filler material; this can be explained as follows. Usually, the yield stress of the filler material is lower than that of the parent materials. Let the joint be subjected to a tensile loading of stress σ1 (Fig. 5.22a). With increasing value of σ1, the filler material tends to yield and the P (parent material)-F (filler material) interfaces tend to resist the yielding (because the parent material does not yield at this loading).
The resulting deformation takes the shape shown in Fig. 5.22b. The yield strength of the filler alloy (σfiller) is determined, by a uniaxial test, when the deformed shape of a rectangular specimen ABCD takes the shape A’B’CD’ (shown by the dashed lines in Fig. 5.22c). If AD and BC are considered as the P-F interfaces (indicated in Fig. 5.22a), then, in the presence of the parent materials, the deformed shape of the same specimen takes the shape A”B”C’’D’’ (Fig. 5.22c) as in Fig. 5.22b.
The deformed shape A”B”C’’D’’ can be obtained from ABCD by the simultaneous application of a constant tensile stress (σ1) on the faces AD and BC, together with the application of a varying lateral tensile stress (σ2) on the faces AB and CD. The magnitude of the lateral stress σ2 maximum at A and B with the minimum (σ2m) occurring at the midpoint of AB.
Now, as σ1 is increased, the joint fails at the midpoint of AB. Using the maximum shear stress theory, we find the joint fails if –
Principle # 2. Adhesive Bonding:
The adhesive bonding process is most commonly used in the aircraft and automobile industries where sheet metals are joined in various configurations. In it, unlike in brazing and soldering, there is no uncertainty about the flow of the adhesive in the joint. This is so because the adhesive is first applied on the surfaces and the joint is made with subsequent application of heat and pressure. However, this advantage should not be overemphasized because of the inherent low strength of the resulting joint.
ADVERTISEMENTS:
Two types of bonding forces take part in an adhesive joint. Of these, one is the van der Waals force due to the constant movement of the positive and the negative charges of molecules. The other is the polar force, between the adhesive and the relatively brittle oxide film, due to the dipole adhesive molecules. This force is normally several orders of magnitude higher than the van der Waals force.
The coefficient of thermal expansion and the elastic properties of the adhesive normally differ very widely from those of the metals to be joined. Therefore, the mechanical properties of an adhesive joint need a careful examination.
The factors that affect the strength and the other mechanical properties of such a joint are:
(i) The nature and dimensions of the joint. The strength of a lap joint increases with the overlapped area and reduces with the joint thickness.
(ii) The contact angle at the solid-liquid interface. In the joint, there is always a possibility of an air bubble getting trapped in the metal cavity. The radius R of the bubble is determined by the size and shape of the cavity together with the contact angle ɸ (Fig. 5.23). It can be shown that the tensile stress necessary to propagate a crack from the cavity is given by –
where Ea, va, and γa are Young’s modulus, Poisson’s ratio, and the surface energy, respectively, of the adhesive.
Moreover, the stress concentration factor due to the formation of a meniscus, shown in Fig. 5.24, depends on the contact angle. The maximum stress concentration factor increases continuously from about 1 to 2.3 as ɸ increases from 0 to 90°.
Up to a value ɸ < 30°, the maximum stress concentration factor and the failure both occur in the body of the adhesive. Beyond ɸ = 30°, the maximum stress concentration factor, and consequently the failure, shift to the interface. The latter situation normally results in lower strength. In actual practice, the adhesive is extruded (by means of external pressure) from the joint to prevent the formation of any meniscus.
(iii) The residual stress and the stress concentration. The adhesive in the joint shrinks due to both cooling and polymerization. This shrinkage results in residual tensile stress in the adhesive, and consequently reduces the strength of the joint.
If a lap joint of two metal sheets of equal thickness t (see Fig. 5.25) is considered, it can be shown that the stress concentration factor in shear due to dissimilar materials is given by –
where Ga is the shear modulus of the adhesive and E is Young’s modulus of the metal. Other factors, e.g., shape and bending of the adhesive, also give rise to stress concentration.