The change in dimensions of forms of matter under the action of applied forces is called ‘deformation’. It is caused either by the mechanical action of external forces or by various physical and physio-chemical processes. To form various metallic shapes the deformation of metals is necessary. The deformed or mechanically worked metals are much superior to cast metals from which they are produced.
Types of Metal Deformation:
The metal deformations are of the following two types:
1. Elastic deformation, and
ADVERTISEMENTS:
2. Plastic deformation.
1. Elastic Deformation:
Elastic deformation is the deformation which disappears when the load is removed. It precedes (takes place before) plastic deformation. This deformation occurs when a stress is applied on a metal piece.
Figs. 3.1 [(i), (ii), (iii)] shows form of the atoms before loading, after loading in tension and compression respectively. When a tensile load is applied, the piece becomes slightly longer whereas a compressive load shortens the piece.
ADVERTISEMENTS:
On removal of load (tensile or compressive) the metal piece or specimen regains its original shape (dimension). Within the elastic range, the strain is result of a slight elongation of the unit cell in the direction of the tensile load, or a slight contraction in the direction of compressive load.
For elastic deformation, the strain is nearly proportional to stress. The ratio between stress and strain under elastic deformation is known as modulus of elasticity or Young’s modulus (E). It is a characteristic of the type of the metal and its magnitude depends upon the force of attraction between atoms of a metal.
Shear stresses are also set up in crystal structures in engineering applications. These produce displacement of one plane of atoms relative to the adjacent plane of atoms. The elastic strain is defined as the tangent of the shear angle. The ratio between shear stress and shear strain is known as shear modulus of rigidity (C).
ADVERTISEMENTS:
It is the deformation which persists even after the load is removed. Plastic deformation is observed at stresses exceeding the elastic limit. In contrast of elastic deformation, which depends primarily on stress in the simplest cases, plastic deformation is typically a function of stress, temperature, and the rate of straining.
Plastic deformation is associated with the displacement of the atoms within the grains and causes ultimately permanent changes in shape of the material. Tensile, compressive and torsional stresses can cause plastic deformation.
Plastic deformation process is generally applied in important metallurgical operations of shaping. The operations include rolling of boiler plates, drawing of wire, extrusion of telephone cables, stamping of automobile parts etc.
ADVERTISEMENTS:
In metals the plastic deformation generally takes place by the process of “slipping”.
Slip:
Slip is defined as a shear deformation that moves atoms by many interatomic distances in one crystal plane over the atoms of another crystal plane. Fig. 3.2 shows the slip process under a shear load (in a single crystal). Because of plastic deformation, the crystal is divided into layers or slip blocks which are displaced in reference to each other and are separated by thin layers in which a considerable displacement of atoms has taken place.
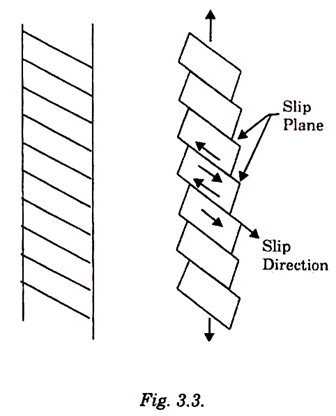
These intermediate layers with strongly distorted lattices are called “slip planes”. Slip occurs more readily along certain crystal directions and planes than along others. This is shown in Fig. 3.3 where a single crystal HCP metal was deformed plastically.
Critical Resolved Shear Stress:
The shear stress required to produce slip on a crystal plane is called the critical resolved shear stress.
For obtaining an expression for shear stress on the slip plane let us consider a crystal subjected to a tensile load (P) acting in the direction of axis (Fig. 3.4). This force P produces a shearing force in the slip plane and a force normal to the slip plane. If β is the angle between the direction of the force and normal to slip plane then area of slip plane will be α/cos β, where A is the cross-sectional area perpendicular to the direction of the force P.
The component of the force P acting in the slip plane in the slip direction = P cos α, where α is the angle between the direction of force and slip direction. ∴
∴ Critical resolved shear stress,
This equation is known as Schimd law. Slip takes place with the minimum axial force when both α and β are 45°. Under these conditions τcr is equal to one half the axial stress P/A. The reduced shear stress is less in relation to the axial stress for any other crystal orientation and as α or β approaches 90° it drops to zero value.
For each material the critical shear stress is a constant and depends on the type of bonding force. It is independent of the relative orientation of the applied stress, the slip direction, hut it is affected by temperature, purity, effect of minor deformation, rate of deformation and surface effects.
The slip will take place if under an applied stress the resolved shear stress reaches the critical value τcr. Under very low rate of deformation some plastic flow is possible in a crystal at shear stress lower than the critical shear stress. This type of deformation is called creep.
I. Critical Resolved Shear Stress (CRSS)
It depends on the following factors:
(i) Composition:
The value of CRSS increases with increasing alloy content,
(ii) Purity:
The value of CRSS increases with increasing impurity content (soluble impurities being more effective than insoluble ones).
(iii) Extent of Prior Deformation:
The value of CRSS increases with increasing amount of prior deformation.
(iv) Temperature:
The value of CRSS generally decreases with increasing temperature and drops abruptly to zero at the melting point or the solidus temperature in alloys. The CRSS is not influenced by the stress normal to the slip plane.
II. Slip:
It effectively consists of a relative displacement of parallel slip planes through the shearing action of the resolved shear stress, and a simultaneous rotation of the active slip system toward the direction of tension.
Although slip resembles simple relative gliding of two parallel planes, it differs in the following respects:
a. Slip is restricted to specific planes and directions with the planes which are determined by internal directional forces.
b. The extent of slip is limited to an inter atomic distance or an integral multiple of that distance. Resistance to continued slip increases (but is essentially constant in gliding).
c. Part of this energy of slip is stored in the crystal as potential (strain) energy in contrast to complete dissipation (as heat) of the energy of gliding.
On a microscopic scale the deformation is not uniform but is localised on slip planes and within slip bands.
The spacing between slip planes in a slip band may be of the order of 200 Å, whereas the separation of adjacent bands may be 100 times as great.
The slip on each plane may be of the order of several microns.
The minimum force necessary to produce slip is several orders of magnitude less than we expect from our knowledge of crystal structures and interatomic forces. In a typical metal, the theoretical critical resolved shear stress is about 1011 dynes/cm2 while the experimental measurement is about 107 dynes/cm2.
Moderate deformation, even at low temperatures, does not drastically alter properties and there is no indication of a breaking-up of the lattice.
As the magnitude of the applied stress increases, the number of active slips planes and the distance of slip along these planes increases.
Sometimes duplex slip occurs particularly in FCC metals. Slip is accompanied by rotation of the slip plane toward the direction of applied tensile stress, and a continued increase in the stress is required for continued deformation. This rotation of the active slip plane toward the axis of tension causes rotation of other slip systems.
If one of these systems rotates into a position in which the resolved shear stress in the system is greater than critical resolved shear stress but less than that required to continue slip on the first system, slip will then take place in the new system. As load increases, slip may take place in both systems by alternating between the two.
Twinning:
Twinning is that process by which a portion of the crystal takes up an orientation which makes that portion a mirror image of the parent crystal.
Deformation by twinning is most common in HCP metals and its effects on others is to move parts of the grains such that they acquire favourable orientation for the slip to occur. Twinning is produced suddenly and is accompanied with sound. The well-known cry of tin is the result of twinning.
Fig. 3.6 shows the classical atomic picture of twinning. The twinning plane is at right angle to the paper. If a shear stress is applied, the crystal will turn about the twinning plane. The region to the left of the twinning plane is un-deformed. To the right of this plane, the planes of atoms have sheared in such a way as to make the lattice a mirror image across the twin plane.
The mechanism of twinning may thus be described as the simple sliding of one plane of atoms over the next, the extent of movement of each plane being proportional to its distance from the twinning plane. Fig. 3.7 shows the schematic representation of twinning.
In case of slip, the offset is a multiple of interatomic spacing, but in twinning the offset produced by sliding of one plane against its neighbour is a fraction of a unit slip. This causes a difference in the orientation between the twinned and untwined regions in the crystal and on polishing and etching these can be easily differentiated under the microscope.
Twins may be of the following two types:
1. Mechanical Twins:
These are produced by mechanical deformation. These are produced in BCC or HCP metals under conditions of rapid rate of loading (shock loading) and decreased temperature.
2. Annealing Twins:
These are produced as a result of annealing following plastic deformation.
About twinning following points are worth noting:
i. Twinning occurs when the atoms in a layer within the crystal are rearranged during deformation in such a manner that the layer develops a mirror image relationship to an adjacent layer of the parent crystal,
ii. The twinning plane is a plane of symmetry relating the twinned layer to the parent crystal.
iii. Although twinning is not actual rotation of planes, it is convenient to visualize the twinned portion of a crystal as if it were rotated about the plane of symmetry. Movement during twinning is really shear of adjacent planes.
All planes involved shift in the same direction, and each plane shifts an amount proportional to its distance from the twinning plane. Thus it is possible to regard twinning as deformation by slip in which every plane of atoms in the twinned layer participates, in contrast to normal slip in which several inclined planes may be found between active planes.
iv. In twinning, each plane of atoms shifts a small but definite fraction of the interplanar spacing with respect to adjacent planes. This shift results in an effective orientation in the twin. This is in contrast to no change of orientation in slip.
v. The twinned section of the crystal may participate in deformation in two ways:
a. Twinning itself may accomplish an extensive change in shape, or
b. It may facilitate further slip by placing planes of potential slip in more favourable positions with respect to the applied stress. The lattice is generally more effective in producing deformation.
vi. The Critical Resolved Shear Stress (CRSS) for twinning (as is the CSSR for slip) is function of composition, purity, prior deformation, and temperature.
Frank Read Source:
It is on a small number of crystal planes that slip occurs intensely and during the process some hundreds of dislocations move. It indicates that some effective creators of dislocations must exist, these are known as Frank Read Sources.
Refer to Fig. 3.29. At first an edge dislocation is anchored at two imperfections. The dislocation line then bulges under the influence of stress in the slip plane, and in a later stage the boundary of original dislocation becomes unstable and curves back around these two points as shown by the stages 1 to 3 in the diagram.
Lastly, in stage 4, there is further spontaneous expansion of the bulge and a closed loop is formed that travels outwards to grain boundary. On disappearance of the loop, the original edge dislocation is again created. If the stress persists another loop is formed and the cycle is repeated.
Frank-Read sources, during cold work, come into operation on each active slip plane and total number of dislocations is increased upto 1012 per square cm.
Deformation of Polycrystalline Materials:
Although the process of deformation is basically the same, the deformation of polycrystalline material is far more complicated. Plastic deformation in a polycrystalline aggregate is never uniform. The greater strength of polycrystalline materials is due to the grain boundaries. The grain boundaries offer more resistance to slip than the interiors of the grains, partly because of the difference in slip direction between the crystals.
Since some of the crystals in a polycrystalline material are always oriented with their slip directions in the plane of maximum shear, they will try to yield to a stress comparable to that for a single crystal. If the surrounding crystals are elastic enough, they will permit minute amount of yielding in these weak crystals. Thus general yielding begins gradually.
Amorphous materials yield by a variety of mechanisms.
Deformation in a polycrystalline metal causes considerable structural changes. In general plastic deformation affects all physio-chemical and mechanical properties of a metal.
Polycrystalline metal shows the following characteristics:
(i) The resolved shear stress varies with grain orientation.
(ii) When such metal/alloy is loaded, various grains do not have the same orientation.
(iii) There are a number of possible slip planes within a crystal.
Stages in the Deformation Process of Polycrystalline Aggregates:
I. All the crystals, under load, are only elastically deformed. The aggregate behaves perfectly elastically.
II. A few crystals pass the elastic limit and deform plastically. If the load is removed, stresses arise between the elastically and plastically deformed crystals which gradually force the plastically deformed crystals back into their original shape. This gradual return is called the “elastic after effect”. Single crystals do not show this effect. If the specimen is repeatedly loaded and unloaded, it gradually work (or strain) hardens throughout and the after effect disappears.
III. In the third stage majority of crystals deform plastically, the material crosses elastic limit and the permanent distortion can be measured.
IV. Finally, plastic deformation in all the crystals becomes considerable, and appreciable yielding of the aggregate sets in.
Mechanism of Deformation (in Polycrystalline Materials):
After the polycrystalline (metal) specimen is loaded, the first deformation takes place by slip in grains that are favourably oriented and then it moves to other grains (although slip from one grain to another is difficult). Where the slip plane meets the grain boundary, a dislocation pile up occurs, producing a stress concentration that helps the movement of dislocation in the next grain across the grain boundary. There is no breakdown of grain coherency and no formation of grain boundary holes, which suggests that there is a change of shape that requires multiple orientation of slip planes.
Whereas, deformation in polycrystalline cubic metals takes place by slip; in hexagonal metals, it occurs only when the applied stress causes twinning.
Yield Point Phenomenon:
Fig. 3.30 shows the stress-strain diagram obtained during tensile deformation when specimen of low carbon steel (annealed) was loaded. The yield point phenomenon was found originally in this material. The first higher point at which yielding starts (U) is called upper yield point and the other lower value (U) having more strain is known as the lower yield point. The stress required to start plastic flow is higher than to maintain plastic flow, as is clear in the diagram, after the yield point is obtained.
Due to dislocations there is work hardening in the specimen. This causes the stress-strain curve to acquire a smooth and gradual rise. This is called the yield point phenomenon which states that the elongation that occurs at constant stress has an important bearing in the yielding strength value.
There is a large strain energy associated with the dislocation of a crystal lattice which will try to reduce it during rearrangement of crystal structure. Impurities also reduce dislocation movements. Thus, a higher stress is needed.
The yield point has significance in the practical use of various metals.
In addition to iron and steel, yield points have been observed in polycrystalline metals like molybdenum, titanium and aluminium alloys.
Yield point has significance, because once the metal yields and the plastic deformation starts in a given area, the metal at this point is effectively softened and suffers a relatively large plastic deformation. This deformation then spreads into the material adjoining the region which has yielded because of the stress concentration at the boundary between the deformed and undeformed areas.
Sharp yield point is very important for a manufacturer who stamps or draws thin sheets of these materials in forming such as automobile bodies and other objects.
Related Effects of Yield Point:
The following are the related effects of yield point:
1. Luders band and stretcher strains.
2. Strain ageing.
3. Blue brittleness.
4. Orange peel effect.
1. Luder Bands:
These are marking on the surface of tensile test specimen formed at the points of stress concentration like fillet. Arrival of the upper yield point is indicated by the formation of these. Actually the lower yield stress is perhaps the stress required to propagate the luder bands.
These bands are generally at approximately 45° to 50° to the tensile axis.
Once a luder band has formed at one fillet of the tensile test specimen, it can move through gauge length of the specimen.
At the specimen passes through the stage of yield point elongation, these bands spread along the specimen and cover the entire gauge length, thereby showing that entire gauge length has been overstrained.
Luder bands frequently occur in drawing and stamping operation when the surface markings in relief are called stretcher strains. In order to avoid these strains on finished parts, the sheets prior to pressing operations are overstrained by means of temper roll pass, so that the yield point phenomenon is eliminated.
Strain ageing implies changes in the properties of an alloy with time after prestraining.
Strain ageing behaviour is usually associated with the yield point phenomenon.
If a test specimen which has been overstrained to remove the yield point is allowed to rest or age after plastic deformation, the yield point returns with a higher stress.
If the specimen is unloaded and retested without ageing then the yield point will occur due to weak dislocation effects from the atmosphere of carbon and hardening due to increase in stress value.
Strain ageing is pronounced in commercial iron and steel, although it proceeds in other metals.
It is an important factor in fatigue and creep behaviour.
This effect is produced when the temperature range of the test is raised; the yield point becomes less pronounced.
Failure of the specimen occurs at low strain with high stress.
The section of the stress-strain diagram shows a steeper curve with rapid formation of successive yield points due to quick diffusion and dislocation effects.
This effect appears at about 160 to 300°C.
These effects (marking) appear on metals during stretching.
It is also a surface roughening phenomenon commonly seen in coarse-grained metals at low temperature-forming operations. Grain refinement eliminates these effects.
Cottrell Theory of Sharp Yield Points:
The sharp yield point observed in many metals is a result of Cottrell theory which states that there are always special atmospheres to reform the interaction between the dislocations and the solute atoms (e.g., carbon, nitrogen, etc.). Such atmospheres anchor the dislocations and higher stresses are required to free a dislocation. The value of this stress should be corresponding to upper yield points. Free dislocations lower the yield point.
Season Cracking:
Season cracking is the defect which is created when internally stressed materials are subjected to corrosive media like industrial atmosphere, ammonia, mercurious nitrate or sea water. Season cracking or stress corrosion cracking results in cracks which grow slowly or rapidly, depending on the environment. The cracks may be intergranular, transgranular or combination of both.
Rate of stress corrosion is affected by the following factors:
(i) Stress level,
(ii) Corrosive agent,
(iii) Time and temperature of exposure,
(iv) Structure of the metal,
(v) Amount of plastic strain, and
(vi) Behaviour of protective film and other factors.
Several theories have been propounded to explain the mechanism of season cracking but it is generally believed that it occurs due to localised electro-chemical corrosion along narrow path, forming local anodic areas in respect to the more cathodic areas of the metal surface.
Although all copper alloys appear to be susceptible to season cracking the liability increases with increasing zinc content. Season cracking often takes place in cartridge brass, but rarely in red brass and other copper alloys of less than 15 percent zinc content.
Season cracking is usually prevented/minimised by proper stress relieving treatment (annealing). For brass the annealing temperature recommended is 300°C.
Bauschinger Effect:
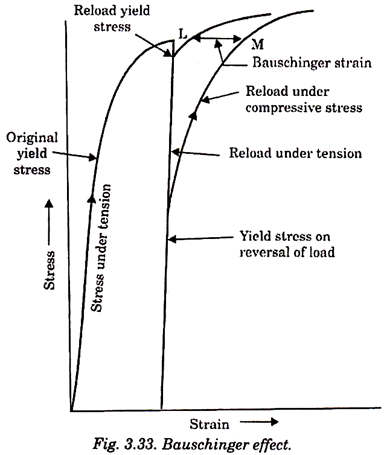
Bauschinger effect is related to the load reversal or cyclic stress. This effect was discovered by Ohann Bauschinger in 1886. Under plastic deformation it would be normally observed that if crystalline materials, say metals are loaded beyond elastic limit and the load is removed and reapplied, the yield strength and proportional limit of the material would have increased.
But if the stress is applied in the opposite direction plastic deformation starts at a lower yield stress than that of the initial deformation. This phenomenon is known as Bauschinger effect (or elastic hysteresis). This is attributed to the presence of residual stresses which cause dislocations to move more easily in the direction opposite to the original, causing strain at a lower stress value.
Fig. 3.33 illustrates the effect of reversal of stress on stress strain curve. The degree of Bauschinger effect is given by LM called Bauschinger strain. Metals that deform by twinning show a large Bauschinger strain.
Bauschinger effect has an important utility in cold working of metals. For example cold rolled steel is strengthened by applying the principle of work hardening. Running a bar of steel through rollers compresses it laterally and causes it to elongate. Elongation causes an increase in tensile yield strength, but lateral compression causes a decrease in tensile yield strength across the bar.
Elastic Aftereffect:
Elastic aftereffect is the time dependence of strain on loading and unloading of a material. Fig. 3.34 illustrates this effect on a strain-line diagram. When a body is subjected to a load an instantaneous strain (e1) occurs which is followed by delayed elastic strain (e2) over a period of time without any further increase in load.
The rate of this increase diminishes and the body stops to deform. On removal of load the material will be relieved of the initial strain e1 but will have strain equal to e2 and gets recovered to its original position asymptotically with time. The phenomenon is known as the elastic aftereffect which is often also called retarded elastic deformation, creep recovery or elastic memory.
The elastic aftereffect is caused partly due to slow evolution of heat due to the stress and diffusion of impurities in pure materials and partly because of mechanical hysteresis effect of the grains.
The mechanism that produces elastic aftereffect is often called internal friction.
It has been observed that between 25 to 90% of the total deformation, depending upon the material, is due to elastic aftereffect.
Thermoelastic Effect:
This is a kind of elastic aftereffect. When a member is elongated, its volume increases, accompanied by a drop in its temperature. This phenomenon is converse of thermal expansion. If elongation takes place slowly enough that thermal equilibrium is maintained, absorption of heat from its surroundings holds the temperature of the member constant and process is isothermal.
If, on the other hand, elongation is rapid and time for heat is insufficient, the process is adiabatic and the temperature of the member is lowered. If over such a member stress is held constant and it is allowed to absorb heat, a farther expansion takes place until the total elongation is the same as in the isothermal process. The two processes are illustrated in Fig. 3.35.
Isothermal elongation is represented by line OM and adiabatic elongation by line OL. This effect is very small and can be detected by very precise measurements. The distance LM as shown is highly exaggerated for explanation purpose. During unloading a similar behaviour is shown; line MO showing isothermal path of unloading whereas ML showing the adiabatic path.
Preferred Orientation:
Non-random alignment of crystals or molecules is known as preferred orientation.
The orientation of grains in individual crystals within a metal is ordinarily random. Cold work such as rolling, wire drawing and swaging destroys this randomness of grain orientation thereby depriving the polycrystalline material of equality of properties in all directions (isotropy).
The grain exhibits now a preferred orientation and the material properties are quite different in various directions (anisotropy). The preferred orientation occurs under plastic deformation and it is a result of the tendency of slip directions in each grain to align themselves with some common direction of deformation.
Fig. 3.36 (b) shows preferred orientation by mechanical work.
Besides being produced by working of metals, preferred orientation can also be seen in cast metals having columnar growth.
Preferred orientation is not generally affected by processing variables such as die angle, roll speed, reduction per pass, etc. The direction of flow is the most important process variable.
Preferred orientations are determined by X-ray methods.
The most significant consequence of preferred orientation of grains in metal is the effect upon elastic properties.
The presence of the preferred orientation can produce undesirable consequences. The strength and related properties of devices formed from such materials reflect the anisotropy of the individual crystallites comprising them. For example, when circular cups are stamped from metal sheets having preferred orientation, the sides of the cups produced are not even, an effect called “earing”.
In many applications, therefore, preferred orientation is to be avoided whenever possible. Sometimes it can be removed from metals by proper annealing following the working of the metal. Conversely it is possible that certain applications require the presence of preferred orientation, for example, the ease of magnetisation of a crystal, depends on the crystallographic direction that is parallel to the magnetic field. Depending upon the desired end result, it may be required to have an easy or a hard direction of magnetisation parallel to a particular direction in the final device.
A few engineering applications for preferred orientations are:
1. Preferred orientation strengthens magnetisation in silicon steels but it is undesirable in others.
2. It results in the loss of ductility particularly in the semi-finished products like sheet metals and wires.
3. Another important application of controlled preferred orientation is in the manufacture of iron sheets for transformer core. Preferred orientation of core iron in the direction of magnetic field saves considerable electrical energy dissipated as heat in the iron core due to eddy currents.
4. The formation of a strong preferred orientation will result in an anisotropy in mechanical properties, i.e., during fabrication, different mechanical properties can be obtained in different directions.
5. In cast metals having columnar growth.
Work (or Strain) Hardening:
Work (or strain) hardening is a phenomenon which results in an increase in hardening and strength of a metal (specimen) subjected to plastic deformation at temperature lower than the recrystallization range (cold working).
When a material is subjected to plastic deformation, a certain amount of work done on it is stored internally as strain energy. This additional energy in a crystal results in strengthening or work hardening of solids.
Thus work (or strain) hardening may be defined as increased hardness accompanying plastic deformation. This increase in hardening is accompanied by an increase in both tensile and yield strength.
Work hardening reduces ductility and plasticity.
Work hardening is used in many manufacturing processes such as rolling of bars and drawing of tubes.
It is also used to improve the elastic strength in the manufacture of many parts such as:
(i) Prestretching of hoisting chains and cables,
(ii) Initial pressurisation of pressure vessel, cylinders of hydraulic press and guns.
Mechanism of Work Hardening:
Work hardening is caused by dislocations interacting with each other and with barriers which impede their motion through the crystal lattice. Hardening due to dislocation interaction is a complicated problem because it involves large groups of dislocations, it is difficult to specify group behaviour in simple mathematical way.
One of the easiest dislocation concepts to explain strain hardening was the ideal that dislocations pile up on slip planes at barriers in crystal. The pile ups produce back stress which opposes the applied stress on slip plane.
Another mechanism of work hardening in addition to that due to back stress resulting from dislocation pile up at barriers, is believed to occur when dislocations moving in the slip plane cut through other dislocations intersecting the slip plane. The dislocations threading through the active slip plane are often called a dislocation forest and this work hardening process is referred to the intersection of a forest of dislocations.
Theory of Work Hardening:
According to all theories (of work hardening) work hardening is due to the increased resistance the dislocations experience in moving through the lattice when the metal has been subjected to cold working/deformation. The basic idea put forward by Taylor in 1934 was that work hardening is due to the dislocations getting in each other’s way. Thus the stress (τ) necessary to move a dislocation in the stress field of other dislocations surrounding it, will have to have a higher value.
Recovery, Recrystallization and Grain Growth:
The deformed metal, in comparison with its underformed state, is in a non-equilibrium and thermodynamically unstable state. Subsequently, spontaneous processes occur in strain- hardened metal, even at room temperature.
If the temperature is raised sufficiently, the metal attempts to approach equilibrium through the processes namely:
(i) Recovery,
(ii) Recrystallization, and
(iii) Grain growth.
Fig. 3.37 shows a schematic drawing indicating recovery, recrystallization and grain growth and changes in important properties in each region.
(i) Recovery:
It is a low temperature phenomenon which results in the restoration of the physical properties without any observable change in microstructure.
During recovery, there is negligible effect on hardness whereas electrical resistance decreases rapidly towards the annealed value.
The process of recovery is important for releasing internal stresses in forging, molded and fabricated equipments, cartridge cases and boiler tubes without decreasing the strength acquired during cold working.
(ii) Recrystallization:
It is a process by which distorted grains of cold worked metal are replaced by new strain free grains during heating above a specific minimum temperature called recrystallization temperature.
Recrystallization temperature is a function of-
(i) Particular metal.
(ii) Purity of Metal – Soluble impurities raise the recrystallization temperature.
(iii) Metal /Alloys – Recrystallization usually occurs at a temperature of about 0.3 Tm in pure metals and about 0.5 Tm, in alloys, where Tm is the melting temperature,
(iv) Amount of Prior Deformation – The greater the degree of cold work the lower the recrystallization temperature and smaller the grain size.
(v) Annealing Time – The longer annealing time decreases the temperature necessary for recrystallization.
(vi) Grain Size – The finer the grain size of cold worked metal, the lower is the recrystallization temperature.
The process of recrystallization can be divided into three states-
(i) Nucleation.
(ii) Primary grain growth.
(iii) Secondary grain growth.
During nucleation small strain free nuclei form at points at crystal grain boundaries in the heated structure.
In the “primary grain growth” the nuclei grow into grains until they first meet, replacing the old grains by new ones, that are now strain free and ultimately “secondary grain growth” which is accompanied with new grain growth at the expense of others and are small in size. During prolonged heating at high temperature the grains grow rapidly and produce locally exaggerated grain growth.
(iii) Grain Growth:
Grain growth is an increase in grain size.
When the material is held for longer times at temperature above crystallization temperature, or when it is heated to a higher temperature the grain size increases and there is decrease in hardness and strength and gain in ductility. The decrease in hardness is not as sharp as during recrystallization.
At a given temperature the grain size D at a given time is given by the following relation known as the law of grain size-
D2 – D20 = C.t
Where, D = Grain size at a given time, D0 = Initial grain size, C = Constant of proportionality, and t = Time.
The process of grain growth depends largely on the following factors:
(i) Annealing temperature.
(ii) Annealing time.
(iii) Rate of heating.
(iv) Degree of prior deformation.
(v) Insoluble properties.
(vi) Alloying elements.
Grain Size Determination:
When the properties of a polycrystalline material are under consideration, the grain size is often determined. In this regard, there exists a number of techniques by which size is specified in terms of average grain volume, diameter or area.
Grain size may be estimated by using an intercept method, described below:
(i) Straight lines, all of the same length, are drawn through several photomicrographs that show the grain structure.
(ii) The grains intersected by each line segment are counted.
(iii) The line length is then divided by an average of the number of grains intersected, taken over all the line segments.
(iv) The average grain diameter is found by dividing this result by the linear magnifications of the photomicrographs.
The most common method utilized is probably that devised by the American Society for Testing and Materials (ASTM). The ASTM has prepared several standard comparison charts, all having different average grain size. To each is assigned a number ranging from 1 to 10, which is termed the grain size number, the larger this number, the smaller the grains.
A specimen must be properly of 100 x. Grain size is expressed as the grain size number of the chart that most nearly matches the grains in the micrograph. Thus, a relatively simple and convenient visual determination of grain size number is possible.
Grain size number is used extensively in the specification of steels.
Cold Working:
A metal is said to be cold worked, if it is mechanically processed below the recrystallization temperature of the metal.
Cold working produces an improved surface finish and closer dimensional tolerance and because of this characteristic cold working processes are generally used in making end- use products.
Since recrystallization does not take place in cold working, the grains are permanently distorted.
During cold working residual stresses are set up. As their presence is undesirable a suitable heat treatment is generally necessary to neutralise these stresses and restore the metal to its original structure.
The various cold working operations are:
1. Drawing
2. Squeezing
3. Bending
4. Shearing
5. Hobbing
6. Shot peening, and
7. Cold extruding.
When there is excessive cold work the metal may fracture before reaching the desired shapes and sizes, and in order to avoid it cold working operations are carried out in several steps.
Hot Working:
When plastic deformation of metal is carried out at temperature above the recrystallization temperature the processes performed on metals are termed as hot working.
Hot working process can be considered as simultaneous combination of cold working and annealing. Any work hardening effect caused by plastic deformation is neutralised immediately by the effect of high temperature.
Hot working process facilitates metal shaping with low power requirements though it is expensive to handle hot materials.
In hot working there is loss of metal by scaling and fine dimensional tolerance cannot be achieved.
Hot working increases the density since any pores or cavities in the cast metal disappear.
Grain structure becomes more refined.
The various hot working operations are:
1. Rolling
2. Forging
3. Pipe welding
4. Hot piercing
5. Hot working
6. Hot spinning, and
7. Hot extruding.