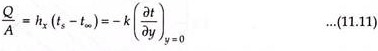When a fluid flows around an object or when the object moves through a body of fluid, there exists a thin layer of fluid close to the solid surface within which shear stresses significantly influence the velocity distribution. The fluid velocity varies from zero at the solid surface to the velocity of free stream flow at a certain distance away from the solid surface.
This thin layer of changing velocity has been called the hydrodynamic boundary layer; a concept first suggested by Ludwig Prandtl in the year 1904. Heat transfer occurs due to heat conduction and energy transport by moving fluid within this thin layer. Hence, the value of convection coefficient and heat transfer is highly dependent upon the thickness and characteristics of the boundary layer.
Hydrodynamic Boundary Layer: Flat Plate:
Consider a continuous flow of fluid along the surface of a thin plate with its sharp leading edge set parallel to flow direction.
The salient features of the flow situation are:
ADVERTISEMENTS:
(i) The free stream undisturbed flow has a uniform velocity U∞ in the x-direction. Particles of fluid adhere to the plate surface as they approach it and the fluid is slowed down considerably. The fluid becomes stagnant or virtually so in the immediate vicinity of the plate surface. Generally it is presumed that there is no slip between the fluid and the solid boundary.
Thus, there exists a region where the flow velocity changes from that of solid boundary to that of mainstream fluid, and in this region the velocity gradients exist in the fluid. Consequently the flow is rotational and shear stresses are present. This thin layer of changing velocity has been called the hydrodynamic boundary layer.
(ii) The condition ∂u/∂y ≠ 0 is true for the zone within the boundary layer, whilst the conditions for flow beyond the boundary layer and its outer edge are-
∂u/∂y = 0 and u = U∞
ADVERTISEMENTS:
Thus all the variation in fluid velocity is concentrated in a comparatively thin layer in immediate vicinity of the plate surface.
(iii) The concepts of boundary layer thickness and outer edge of the boundary layer are quite fictitious as there is no abrupt transition from the boundary layer to the flow beyond or outside it. Velocity within the boundary layer approaches the free stream velocity asymptotically. Usually the boundary layer thickness δ is taken to be the distance from the plate surface to a point at which the velocity is within 1 percent of the asymptotic limit, i.e., u = 0.99 U∞.
The parameter 8 then becomes a nominal measure of the thickness of boundary layer, i.e., of the region in which the major portion of velocity deformation takes place. The thickness is me a -j red normal to the plate thickness. The boundary layer is normally very thin in comparison with the dimensions of the body immersed in the flow.
(iv) The thickness of the boundary layer is variable along the flow direction; it is zero at leading edge of the plate and increases as the distance x from the leading edge is increased. This aspect may be attributed to the viscous forces which dissipate more and more energy of the fluid stream as the flow proceeds. Consequently, a large group of the fluid particles is slowed down.
ADVERTISEMENTS:
The boundary layer growth is also governed by other parameters such as the magnitude of the incoming velocity and the kinematic viscosity of the flowing fluid. For higher incoming velocities, there would be less time for viscous forces to act and accordingly there would be less quantum of boundary layer thickness at a particular distance from the leading edge. Further, the boundary layer thickness is greater for the fluids with greater kinematic viscosity.
(v) For some distance from the leading edge, the boundary layer is laminar and the velocity profile is parabolic in character. Flow within the laminar boundary layer is smooth and the streamlines are essentially parallel to the plate. Subsequently the laminar boundary layer becomes unstable and the laminar flow undergoes a change in its flow structure at a certain point, called transition point, in the flow field. Within a transition zone, the flow is unstable and is referred to as transition flow. After going through a transition zone of finite length, the boundary layer entirely changes to turbulent boundary layer.
(vi) The turbulent boundary layer does not extend to the solid surface. Underlying it, an extremely thin layer, called laminar sub-layer, is formed wherein the flow is essentially of laminar character. Outside the boundary layer, the main fluid may be either laminar or turbulent.
(vii) The pattern of flow in the boundary layer is judged by the Reynolds number Re = U∞x/v where x is distance along the plate and measured from its leading edge. The transition from laminar to turbulent pattern of flow occurs at values of Reynolds number between 3 × 105 to 5 × 105. Besides this critical Reynolds number, the co-ordinate points at which deterioration of the laminar layer begins and stabilized turbulent flow sets in is dependent on the surface roughness, plate curvature and the pressure gradient, and the intensity of turbulence of the free stream flow.
ADVERTISEMENTS:
(viii) In a laminar boundary layer, the velocity gradient becomes less steep as one proceeds along the flow. It is because now the change in velocity from no slip at the plate surface to free stream value in the potential core occurs over a greater transverse distance. Nevertheless in a turbulent boundary layer, there occurs an interchange of momentum and energy amongst the individual layers comprising the boundary layer. Consequently, a turbulent boundary layer has a fuller velocity profile and a much steeper velocity gradient at the plate surface when compared to those for a laminar boundary layer.
(ix) Velocity gradient and hence the shear stress has a higher value at the plate surface. For a laminar boundary layer the velocity gradient becomes smaller along the flow direction and so does the shear stress. However for a turbulent boundary layer the shear stress at the plate surface again takes up a high value consistent with the steeper velocity gradient.
(x) Development of boundary layer for pipe flow proceeds in a fashion similar to that for flow along a flat plate. However boundary layer is limited to the pipe radius because of the flow being within a confined passage. Boundary layers from the pipe walls meet at the center of the pipe and the entire flow acquires the characteristics of a boundary layer.
Beyond this point, the velocity profile does not change and it is said to constitute a fully-developed flow. Further, the velocity gradient and the wall shear stresses are greatest at the pipe entrance and drop to a steady value at and beyond the region of fully-developed flow. The characteristic velocity distribution of fully developed laminar and turbulent boundary layer flow inside a pipe are depicted in Fig. 11.3.
The entrance length required for the flow to become fully-developed turbulent flow is dependent on the surface finish, initial level of turbulence, downstream conditions, and fluid properties and is generally estimated to be 50-80 times the pipe diameter.
For hydraulic boundary layers, the following results are of particular interest:
(i) The boundary layer thickness δ is taken to be the distance from the plate surface to a point at which the velocity is within 1% of the asymptotic limit, i.e., u = 0.99 U∞.
(ii) The local skin friction coefficient Cfx refers to the ratio of the local wall shear stress t. to the dynamic pressure of the uniform flow stream.
Depending upon the nature of velocity profile, the values of boundary layer thickness and skin friction coefficient are:
In the above identities Rex = x ρ U∞/µ is the Reynolds number based on distance x from the leading edge of the plate.
An estimate of the average value of skin friction coefficient C͞f can be made by integrating the local skin friction coefficient Cf from x = 0 to x = l (where l is the length of plate) and then dividing the integrated result by the plate length,
Where, Rel is the Reynolds number based upon total length I of the plate. The average skin friction coefficient is quite often referred to as drag coefficient.
Example 1:
Atmospheric air at 25°C flows parallel to a flat plate at a velocity of 3 m/s. Use the exact Blasius solution to estimate the boundary layer thickness and the local skin friction coefficient at x = 1 m from the leading edge of the plate. How these values would compare with the corresponding values obtained from the approximate von-Karman integral technique? Assume cubic velocity profile.
Solution:
For air at 25°C, v = 15.33 × 10-6 m2/s and therefore the Reynolds number is
Thermal Boundary Layer:
When a fluid flows past a heated or cold surface, a temperature field is set up in the fluid next to the surface. If the plate surface is hotter than the fluid, the temperature distribution will be as indicated in Fig. 11.3. Usually the temperature field encompasses a very small region of fluid, i.e., the region of fluid being heated by the plate is confined to a thin layer near the surface. This zone or thin layer wherein the temperature field exists is called the thermal boundary layer. The temperature gradient results due to heat exchange between the plate and the fluid.
The thickness δf of thermal boundary layer is arbitrarily defined as the distance y from the plate surface at which-
The convection of energy reduces the outward conduction in the fluid and consequently the temperature gradient decreases away from the surface. Further, the temperature gradient is infinite at the leading edge of the plate and approaches zero as the layer develops downstream. Moreover in the turbulent boundary layer, the action of eddies flattens the temperature profile.
If the approaching free stream temperature t∞ is above the plate surface temperature ts, the thermal boundary layer will have the shape as depicted in Figure 11.4. The temperature of the fluid changes from a minimum at the plate surface to the temperature of the mainstream at a certain distance from the surface.
At point A, the temperature of the fluid is the same as the surface temperature ts. The fluid temperature increases gradually until it acquires the free stream temperature t∞.The distance AB, measured perpendicularly to the plate surface, denotes the thickness of thermal boundary at a distance x from the leading edge of the plate.
The concept of thermal boundary layer is analogous to that of hydrodynamic boundary layer; the parameters affecting their growth are, however, different. The velocity profile of the hydrodynamic boundary layer is dependent primarily upon the viscosity of the fluid.
In a thermal boundary layer the temperature profile depends upon the flow velocity, specific heat, viscosity and thermal conductivity of the fluid. The thermo-physical properties of the fluid affect the relative magnitude of δ and δt, and the non-dimensional Prandtl number (Pr = µ cp/k) constitutes the governing parameter-
(i) When Pr = 1 δt = δ
(ii) When Pr > 1 δt < δ
(iii) When Pr < 1 δt > δ
The dimensionless temperature distribution for various values of Prandtl number has been shown plotted in Fig. 11.5; the curves for Pr = 0.7 is typical for air and several other gases.
The following results are of practical interest:
(i) The thickness of thermal boundary layer 8f is taken to be the distance from the plate surface for which
ts – t/ts – t∞ = 0.99
For this value of non-dimensional temperature parameter, there are several curves with different values of Prandtl number.
The thickness of thermal boundary layer is thus proportional to with increase in distance from the leading edge, the effects of heat transfer penetrate further into the free stream and the thermal boundary layer grows. Comparison of equations 11.4 and 11.7 reveals that when Pr = 1, the thermal and hydrodynamic boundary layers are of equal thickness and that the temperature and velocity surfaces are identical. Since Prandtl number for most gases are sufficiently close to unity (0.6 < Pr < 1.0), the two boundary layers would be very close for the gases.
Apparently the thermal boundary layer is thicker than the hydrodynamic boundary layer for the flow situations with Pr < 1. This has to be so because Pr < 1 implies that thermal diffusivity is more than the momentum diffusivity. A large thermal diffusivity means more penetration of the temperature effects and consequently a large value of the thermal boundary layer thickness.
Apparently δt < δh when Pr > 1.
Pohlhausen has suggested the following general correlation between Prandtl number and the relative values of thermal and hydrodynamic boundary layer thicknesses.
δt = δh (Pr)-0.33 …(11.10)
(ii) The heat flux at the surface may be written as-
This expression is quite appropriate because at the plate surface, there is no fluid motion and the heat transfer can occur only through conduction.
Through rigorous mathematics analysis, it has been suggested by Prandtl that temperature gradient may be prescribed as-
Equations 11.12 and 11.13 relate local values of the convective coefficient and the Nusselt number; these apply at a specific value of distance x from the leading edge of the plate.
Taking averages over the interval 0 < x < I, we can work out the average heat transfer coefficient and Nusselt number to be;
The bar over the quantity indicates its average value.
For setting up an expression for the convective heat transfer coefficient for laminar flow over a flat plate that has an unheated starting length x0, we adopt the following sequence-
(i) The velocity profile within the boundary layer is taken to be of the cubic form-
(ii) The temperature distribution within the boundary layer satisfies the conditions-
(iii) The appropriate identities for the velocity and temperature distributions are inserted into the integral energy equation. This leads to the following correlation between δt (thermal boundary layer thickness) and δ (hydrodynamic boundary layer thickness)
If heating of the plate starts from the leading edge of the plate itself, i.e., when the plate is heated over the entire length, x0 = 0-
The local heat transfer coefficient hx can be worked out from the equality,
From the expression for temperature distribution –
The foregoing analysis is valid only for laminar conditions. With increase in length of the plate, the flow may have transition from laminar to turbulent conditions. Apparently then a limit needs to be imposed on the plate length along the flow direction.
Example 2:
A small thermo-couple is positioned in a thermal boundary layer near a flat plate past which water flows at 30°C and 0.15 m/s. The plate is heated to a surface temperature of 50°C and at the location of the probe, the thickness of thermal boundary layer is 15 mm. If the temperature profile as measured by the probe is well-represented by-
Determine (a) the heat flux from plate to water; and (b) the heat transfer coefficient.
Solution:
At the mean film temperature tf = (30 + 50)/2 = 40°C, the thermal conductivity of water is 0.633 W/m-deg.