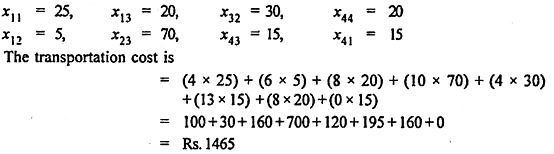Balanced and Unbalanced Transportation Problem | Operations Research

After reading this article you will learn about balanced and unbalanced transportation problem.

Balanced Transportation Problem:

For a transportation problem:

Minimise z = 

Subjected to constraints

x₁₁ for all i and j is said to be balanced transportation problem when total supply from all the sources is equal to the total demand in all destinations, otherwise, problem is said to be unbalanced transportation problem.

A transportation problem may have feasible solution only it is a balanced problem. An unbalanced problem can be made balanced by adding dummy supply centre (row) or dummy demand centre as per the requirement.

Unbalanced Transportation Problem:

If in a transportation problem, the sum of supply available from all sources is not equal to the sum of demands of all destinations, i.e. the problem is said to be unbalanced transportation problem.

But for a feasible solution to exist, total supply must be equal to the total demand thus it is necessary to convert these unbalanced T.P. into balanced one.

There are two possibilities:

Supply is in excess than the demand, we introduce a dummy demand centre (additional destination column) to the transportation problem to absorb the excess supply. The unit transportation cost for the cells of this dummy destination column are all set equal to zero, because these represents item that are not being made and sent.

Working Rule:

Whenever i.e. total demand exceeds total supply, we introduce a dummy supply centre (additional supply row) in the transportation problem to meet extra demand. The unit transportation cost for the cells of its dummy row are set equal to zero.

Example of Second Type:

Solve the transportation problem when the unit transportation costs, demand and supplies are as given below.

Solution:

Since the total demand ∑b_j = 215 is greater than the total supply ∑ a_i = 195 the problem is an unbalanced T.P.

We convert this into a balanced T.P. by introducing a dummy origin 0₄ with cost zero and giving supply equal to 215 – 195 = 20 units. Hence we have the converted problem as follows.

As this problem is balanced there exists a feasible solution to this problem. Using least cost method we get the following initial solution:

There are 7 independent non – negative allocation equals to m + n— 1. Hence, the solution is a non – degenerate one.

The total transportation cost

= (6 x 65) + (5 x 1)+(30 x 5)+(25 x 2)+(4 x 25) + (7 x 45) +(20 x 0)

= Rs. 1010

To find the optimal solution:

We apply the steps in MODI method to the above table.

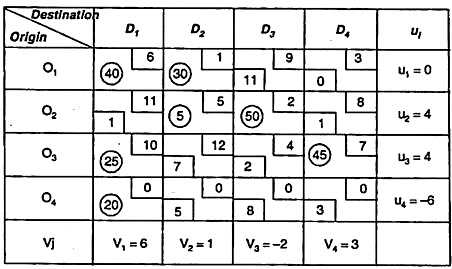
First of all we calculate u₁ v_j & Δ_ij.

using the relation c_ij = u_i + v_j for occupied cells

and Δ_ij = c_ij – ( u_i+ v_j) for unoccupied cells.

Since all Δ_ij is not greater or equal to zero then solution is not optimum.

.^.. We introduce the cell (O_3, D₁) as this cell has most negative value of Δ_ij, Hence this cell is selected to be brought into basis.

For cell O₃ D₁ we construct closed path as follows

O₃D₁→O₃D₃→O₂D₃→ O₂D₂→O₁D₂→ O_xD₁→O₁D₁→O₃D₃

We assign (+) and minus (-) alternately on the closed path starting (+) for the selected all O₂D₁, and adjusting relevant supplies/demand position, the revised allocation will be following table.

As the no of independent allocations are equal to m + n – 1, we check the optimality for this we again calculate u_e u_j & Δ_ij.

Example of First type:

A product is produced by four factories F₁, F₂, F₃ and F₄. Their unit production cost are Rs 2, 3, 1 and 5 respectively. Production capacity of the factories are 50, 70, 30 and 50 units resp. The product is supplied to 4 stores S₁, S₂, S₃, and S₄, the requirements of which are 25, 35, 105 and 20 resp. Unit cost of transportation are given below.

Find the transportation plan such that the total production and transportation cost is minimum.

Solution:

We form the transportation table which consists of both production and transportation. costs.

This table is as follows:

Where total cost = unit cost of production + transportation cost

Hence the problem is unbalanced. We convert it into a balanced one by adding a dummy store S₅ with cost 0 and the excess supply is given as the rim requirement to this store namely (220 — 185) =15 units

To find initial basic feasible solution:

The initial basic feasible solution is obtained by least cost method, and we have found following initial basic feasible solution.

The initial basic feasible solution containing m + n – 1=8 non-negative independent allocation. So the solution is non – degenerate solution.

The total transportation cost

= (4 x 25)+(6 x 5)+(8 x 20)+(10 x 50)+ (8 x 20)+ (4 x 30) +(13 x 35) + (15 x 0)

= Rs. 1525

To find the optimal solution:

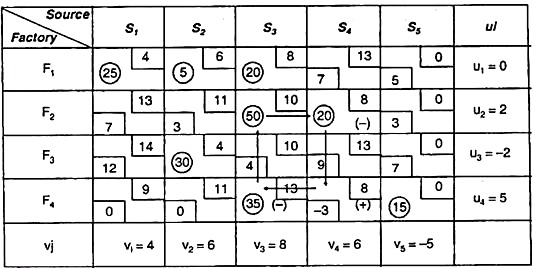
For this we apply MODI method to the above table as it has m + n – 1 independent non – negative allocation for this first we calculate u_i, v_j and Δ_ij with following relation

C_ij = u_i + v_j for occupied cell

Δ_ij = c_ij – (u_i + v_j) for unoccupied cell

This solution is not optimum since cell (F₄, S₄) is having a negative net evaluation value i.e. Δ₄₄ = -3

Then we draw a closed path from the cell and have a modified allocation by adding and subtracting min = (35,20) = 20.

This closed path is F₄S₄ → F₄S₃ → F₂S₄ → F₂S₄ → F₄S₄

This modified allocation is given in the following table:

Again we have check optimality for the again we calculate u_i, v_j & Δ_ij.

Since all values of Δ_ij ≥ o the solution is optimum.

The optimum solution is