After reading this article you will learn about: 1. Definition of Curves 2. Classification of Curves 3. Various Parts 4. Elements 5. Designation 6. Methods 7. Transition Curve.
Definition of Curves:
Curves are regular bends provided in the lines of communication like roads, railways etc. and also in canals to bring about the gradual change of direction. They are also used in the vertical plane at all changes of grade to avoid the abrupt change of grade at the apex.
Curves provided in the horizontal plane to have the gradual change in direction are known as Horizontal curves, whereas those provided in the vertical plane to obtain the gradual change in grade are known as vertical curves. Curves are laid out on the ground along the centre line of the work. They may be circular or parabolic.
Classification of Curves:
(i) Simple,
ADVERTISEMENTS:
(ii) Compound
(iii) Reverse and
(iv) Deviation
(i) Simple Curve:
ADVERTISEMENTS:
A simple curve consists of a single arc of a circle connecting two straights. It has radius of the same magnitude throughout. In fig. 11.1 T1 D T2 is the simple curve with T1O as its radius.
(ii) Compound Curve:
A compound curve consists of two or more simple curves having different radii bending in the same direction and lying on the same side of the common tangent. Their centres lie on the same side of the curve. In fig. 11.2, T1 P T2 is the compound curve with T1O1 and PO2 as its radii.
(iii) Reverse (or Serpentine) Curve:
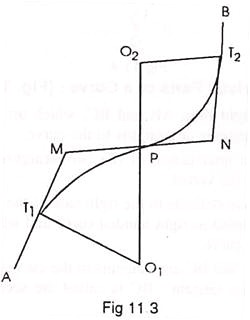
A reverse or serpentine curve is made up of two arcs having equal or different radii bending in opposite directions with a common tangent at their junction. Their centres lie of opposite sides of the curve. In fig. 11.3 T1 P T2 is the reverse curve with T1O1 and PO2 as its radii.
Reverse curves are used when the straights arc parallel or intersect at a very small angle. They are commonly used in railway sidings and sometimes on railway tracks and roads meant for low speeds. They should be avoided as far as possible on main railway lines and highways where speeds are necessarily high.
ADVERTISEMENTS:
(iv) Deviation Curve:
A deviation curve is simply a combination of two reverse curves. It is used when it becomes necessary to deviate from a given straight path in order to avoid intervening obstructions such as a bend of river, a building, etc. In fig. 11.4. T1 EDFT2 is the deviation curve with T1O, EO2 and FO2 as its radii.
Names of Various Parts of a Curve: (Fig. 11.5):
(i) The two straight lines AB and BC, which are connected by the curve are called the tangents or straights to the curve.
ADVERTISEMENTS:
(ii) The points of intersection of the two straights (B) is called the intersection point or the vertex.
(iii) When the curve deflects to the right side of the progress of survey as in fig. 11.5, it is termed as right handed curve and when to the left, it is termed as left handed curve.
(iv) The lines AB and BC are tangents to the curves. AB is called the first tangent or the rear tangent BC is called the second tangent or the forward tangent.
(v) The points (T1 and T2) at which the curve touches the tangents are called the tangent points. The beginning of the curve (T1) is called the tangent curve point and the end of the curve (T2) is called the curve tangent point.
(vi) The angle between the tangent lines AB and BC (ABC) is called the angle of intersection (I)
(vii) The angle by which the forward tangent deflects from the rear tangent is called the deflection angle (ɸ) of the curve.
(viii) The distance the two tangent point of intersection to the tangent point is called the tangent length (BT1 and BT2).
(ix) The line joining the two tangent points (T1 and T2) is known as the long-chord
(x) The arc T1FT2 is called the length of the curve.
(xi) The mid-point (F) of the arc (T1FT2) in called summit or apex of the curve.
(xii) The distance from the point of intersection to the apex of the curve BF is called the apex distance.
(xiii) The distance between the apex of the curve and the midpoint of the long chord (EF) is called the versed sine of the curve.
(xiv) The angle subtended at the centre of the curve by the arc T1FT2 is known as the Central angle and is equal to the deflection angle (ɸ).
Elements of a Curve (Fig. 11.5):
Designation of Curves:
A curve may be designated either by the radius or by the angle subtended at the centre by a chord of particular length In India, a curve is designated by the angle (in degrees) subtended at the centre by a chord of 30 metres (100 ft.) length. This angle is called the degree of the curve (D).
The relation between the radius and the degree of the curve may be determined as follows:
Refer to fig 11.6:
Let R= The radius of the curves in meters
D= The degree of the curve
MN= The chord, 30m long
P= The mid-point of the chord
The approximate relation holds good up to 5° curves. For higher degree curves, the exact relation should be used.
Methods of Curve Ranging:
A curve may be set out:
1. By linear methods, where chain and tape are used.
2. By angular or instrumental methods, where a theodolite with or without a chain is used.
Before starting setting out a curve by any method, the exact positions of the tangent points between which the curve lies, must be determined.
For this, proceed as follows: (Fig. 11.5)
(i) Having fixed the directions of the straights, produce them to meet at point (B).
(ii) Set up a theodolite at the intersection point (B) and measure the angle of intersection (I). Then find the deflection angle (ɸ) by subtracting (I) from 180°. i.e., ɸ = 180° — I
(iii) Calculate the tangent length from the Eqn. 11.3:
(iv) Measure the tangent length (BT1) backward along the rear tangent BA from the intersection point B, thus locating the position of T1.
(v) Similarly, locate the position of T2 by measuring the same distance forward along the forward tangent BC from B,
Having located the positions of the tangent points T1 and T2; their changes may be determined. The change of T1 is obtained by subtracting the tangent length from the known change of the intersection point B. And the change of T2 is found by adding the length of the curve to the change to T1.
Then the pegs are fixed at equal intervals on the curve. The interval between the pegs is usually 30 m or one chain length. This distance should actually be measured along the arc, but in practice it is measured along the chord, as the difference between the chord and the corresponding arc is small and hence negligible. In order that this difference is always small and negligible, the length of the chord should not be more than 1/20th of the radius of the curve. The curve is then obtained by joining all these pegs.
The distances along the centre line of the curve are continuously measured from the point of beginning of the line upto the end, i.e., the pegs along the centre line of the work should be at equal interval from the beginning of the line to the end. There should be no break in the regularity of their spacing in passing from a tangent to a curve or from a curve to a tangent.
For this reason, the first peg on the curve is fixed at such a distance from the first tangent point (T1) that its change becomes the whole number of chains i.e. the whole number of peg interval. The length of the first chord is thus less than the peg interval and is called as a sub- chord. Similarly there will be a sub chord at the end of the curve. Thus a curve usually consists of two-chords and a number of full chords. This is made clear from the following example.
Transition Curves:
A non-circular curve of varying radius introduced between a straight and a circular curve for the purpose of giving easy changes of direction of a route is called a transition or easement curve. It is also inserted between two branches of a compound or reverse curve.
Advantages of providing a transition curve at each end of a circular curve:
(i) The transition from the tangent to the circular curve and from the circular curve to the tangent is made gradual.
(ii) It provides satisfactory means of obtaining a gradual increase of super-elevation from zero on the tangent to the required full amount on the main circular curve.
(iii) Danger of derailment, side skidding or overturning of vehicles is eliminated.
(iv) Discomfort to passengers is eliminated.
Conditions to be fulfilled by the transition curve:
(i) It should meet the tangent line as well as the circular curve tangentially.
(ii) The rate of increase of curvature along the transition curve should be the same as that of increase of super-elevation.
(iii) The length of the transition curve should be such that the full super-elevation is attained at the junction with the circular curve.
(iv) Its radius at the junction with the circular curve should be equal to that of circular curve.
There are three types of transition curves in common use:
(1) A cubic parabola,
(2) A cubical spiral, and
(3) A lemniscate, the first two are used on railways and highways both, while the third on highways only.
When the transition curves are introduced at each end of the main circular curve, the combination thus obtained is known as combined or Composite Curve.
Super-Elevation or Cant:
When a vehicle passes from a straight to a curve, it is acted upon by a centrifugal force in addition to its own weight, both acting through the centre of gravity of the vehicle. The centrifugal force acts horizontally and tends to push the vehicle off the track.
In order to counteract this effect the outer edge of the track is super elevated or raised above the inner one. This raising of the outer edge above the inner one is called super elevation or cant. The amount of super-elevation depends upon the speed of the vehicle and radius of the curve.
Let:
W = the weight of vehicle acting vertically downwards.
F = the centrifugal force acting horizontally,
v = the speed of the vehicle in metres/sec.
g = the acceleration due to gravity, 9.81 metres/sec2.
R = the radius of the curve in metres,
h = the super-elevation in metres.
b = the breadth of the road or the distance between the centres of the rails in metres.
Then for equilibrium, the resultant of the weight and the centrifugal force should be equal and opposite to the reaction perpendicular to the road or rail surface.
If θ is the inclination of the road or rail surface, the inclination of the vertical is also θ
Characteristics of a Transition Curve (Fig 11.25):
Here two straights AB and BC make a deflection angle ∆, and a circular curve EE’ of radius R, with two transition curves TE and E’T’ at the two ends, has been inserted between the straights.
(i) It is clear from the figure that in order to fit in the transition curves at the ends, a circular imaginary curve (T1F1T2) of slightly greater radius has to be shifted towards the centre as(E1 EF E E1. The distance through which the curve is shifted is known as shift (S) of the curve, and is equal to , where L is the length of each transition curve and R is the radius of the desired circular curve (EFE’). The length of shift (T1E1) and the transition curve (TE) mutually bisect each other.
Fig. 11.25:
(ii) The tangent length for the combined curve
(iv) The central angle for the circular curve:
∠EOE’=∆2ɸ1
(v) Length of the circular curve EFE’
(vi) Length of the combined curve TEE’T”
(vii) Change of beginning (T) of the combined curve = Change of the intersection point (B)-total tangent length for the combined curve (BT).
(viii) Change of the junction point (E) of the transition curve and the circular curve = Change of T + length of the transition curve (L).
(ix) Change of the other junction point (E’) of the circular curve and the other transition curve-change of E + length of the circular curve.
(x) Change of the end point (T’) of the combined curve = change of E’ + length of the transition curve.
Check:
The change of T thus obtained should be = change of T + length of the combined curve.
Note:
The points on the combined curve should be pegged out with through change so that there will be sub-chords at each end of the transition curve and of the circular curve.
(xi) The deflection angle for any point on the transition curve distant I from the beginnings of combined curve (T),
Check:
The deflection angle for the full length of the transition curve:
(xii) The deflection angles for the circular curve are found from:
Check:
The deflection angle for the full length of the circular curve:
(xiii) The offsets for the transition curve are found from:
(xiv) The offsets for the circular curve from chords producers are found from:
Method of Setting Out Combined Curve by reflection Angles (Fig. 11.25):
The first transition curve is set out from T by the deflection angles and the circular curve from the junction point E. The second transition curve is then set out from T’ and the work is checked on the junction point E’ which has been previously fixed from E.
(i) Assume or calculate the length of the transition curve.
(ii) Calculate the value of the shift by:
(iii) Locate the tangent point T by measuring backward the total tangent length BT (article 11.14, ii) from the intersection point B along BA, and the other tangent T by measuring forward the same distance from B along BC.
(iv) Set up a theodolite at T, set the vernier A to zero and bisect B.
(v) Release the upper clamp and set the vernier to the first deflection angle (x1) As obtained from the table of deflection angles, the line of sight is thus directed along the first point on the transition curve. Place zero end of the tape at T and measure along this line a distance equal to first sub chords, thus locating first point on the transition curve.
(vi) Repeat the process, until the end of the curve E is reached.
Check:
The last deflection angle should be equal to φ1/3, and the perpendicular offset from the tangent TB for the last point E should be equal to 4S.
Note:
The distance to each of the successive points on the transition curve is measured from T.
(vii) Having laid the transition curve, shift the theodolite to E and set it up and level it accurately.
(viii) Set the vernier to a reading(360°-2/3 φ1 ) for a right-hand curve (or 2/3 φ1) for a left-hand curve and lake a back sight on T. Loosen the upper clamp and turn the telescope clockwise through an angle 2/3 φ1 the telescope is thus directed towards common tangent at E and the vernier reads 360°. Transit the telescope, now it points towards the forward direction of the common tangent at E i.e. towards the tangent for the circular curve.
(ix) Set the vernier to the first tabulated deflection angle for the circular curve, and locate the first point on the circular curve as already explained in simple curves.
(x) Set out the complete circular curve up to E’ in the usual way
Check:
The last deflection angle should be equal to
(xi) Set out the other transition curve from T as before. The point E’ to be set from T should be the same as already set out from E.
Method of Setting Out a Combined Curve by Tangential Offsets (Fig. 11.25):
(i) Assume or calculate the length of the transition curve.
(ii) find the value of the shift train, .
(iii) Locate the tangent points T and T as in article (11.15, iii),
(iv) Calculate the offset for the transition curve as in article (11.14 xiv)
(v) Locate die points on the transition curve as well as on the circular curves by setting out the respective offsets.