After reading this article you will learn about the types and characteristics of vertical curves.
Vertical curves are introduced at changes of gradient to avoid impact and to maintain good visibility. These are set out in a vertical plane to round off the angle and to obtain a gradual change of gradient. The vertical curves may be circular or parabolic but the later are commonly used.
For small gradient angles, the difference between a circular and a parabolic curve is negligibly small. Vertical curves are called summit curves if they have convexity upwards and valley curves if they have concavity upwards.
Types of Vertical Curves:
(i) An upgrade followed by a down grade (fig 11.26):
(ii) An upgrade followed by another upgrade (Fig. 11.27, a &b):
(iii) A down grade followed by an upgrade (fig 11.28):
ADVERTISEMENTS:
(iv) A down grade followed by another down grade (fig. 11.29 a & b):
Characteristics of Vertical Curves:
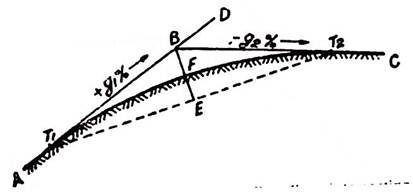
In Fig 11.30, AB and BC are two gradient lines intersecting at BA vertical curve (T1FT2) is to be introduced between these gradients.
Let:
g1% = the gradient of line AB (In this case, it is +ve).
g2% = the gradient of line BC (In this case, it is -ve).
ADVERTISEMENTS:
T1 and T2 = the tangent points to the curve, T1 is the beginning of the curve and T2 is the end of the curve.
T1 and T2 = the line joining the points of tangency or the chord of the curve.
E = the mid-point of the chord of the curve.
F = the mid-point of the curve.
ADVERTISEMENTS:
(i) It is assumed that length of the vertical curve is equal to the length of the two magnets i.e. T1FT2 = BT1 + BT2
The length of the curve on either side of the intersection point is also assumed to the equal i.e, half of the length on one side and the remaining half on other side of the intersection point.
(ii) Change of beginning of the curve (T1)
= Change of intersection point – half the length of the vertical curve.
= Change of B – L/2
(iii) Change of end of the curve (T2)
= Change of the intersection point + half the length of the vertical curve.
= Change of B + 172
(iv) R.L. of T1 = R.I. of B ± Level difference between T1 and B. (+ve sign will be used if g1 is -ve and vice versa.) In this case g1 is +ve, ∴ – ve sign is to be used
(v) R.L. of T2 = R.L. of B ± Level difference between B and T2 (+ve sign will be used if g2 is +ve and -ve if g2 is -ve). In this case g2 is ∴-ve, -ve sign is to be used
(vii) It is well known property of parabola that midpoint E of the chord T1T2 is situated on the vertical through the point of intersection B of the two tangents, and that mid-point F of the vertical curve is midway between these two points
(viii) The curve length on either side of the intersection point is divided into suitable number of parts (15m, 20m, or 30m) and the reduced levels of the points on the curve may be calculated by adding algebraically the tangent corrections (tangent offsets) to the reduced levels of the corresponding points on the tangent.
R.L. of a point at a distance x on the curve
= R.L. of the point at a distance x long the tangent ± tangent correction (yx).
(a) R.Ls of the points along the tangent can be determined from the known values of the R.L. of the tangent point or intersection point and the gradient of the tangent lines.
R.L. of a point at a distance x from the tangent point
(b) Tangents correction (tangent offset) for a point at a distance x along the tangent:
(ix) The result may be tabulated as under: