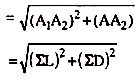Adjustment of a Closed Traverse | Theodolite Surveying

Adjustment of a closed traverse includes: 1. Adjustment of Angular Error. 2. Adjustment of Bearings. 3. Adjustment of Closing Error.

1. Adjustment of Angular Error:

(a) Angular Error:

The theoretic sum of the interior angles of a traverse should equal (2N-4) right angles, and that of the exterior angles should equal (2N+4) right angles, where N is the number of sides of a closed traverse. The difference between the theoretic sum and the sum of the measured angles in a closed traverse is called the angular error of closure. It should not exceed the least count x√N.

(b) Adjustment:

ADVERTISEMENTS:

When all angles are measured with equal care and under similar conditions, this error is distributed equally among all the angles. However, if the accuracy of some angle or angles is suspected due to peculiar field conditions, the whole or the most of the angular error may be assigned to that angle or angles.

2. Adjustment of Bearings:

(a) Closing Error in Bearings:

If traversing is done by taking bearings of the lines, the closing error in bearing may be determined by comparing the back and fore bearings of the last line of the closed traverse as observed at the first and last stations of the traverse respectively. When the traverse ends on a line of known bearing, the error in bearing may be determined by finding the difference between its observed bearing and known bearing.

(b) Adjustment:

ADVERTISEMENTS:

If e is the closing error in bearing, and N is the number of the sides of the traverse, then the correction applied to the bearings of the sides are:

Correction to the Bering =e/N

‘‘ ‘‘ second ‘‘ = 2e/N

‘‘ ‘‘ third ‘‘ = 3e/N

ADVERTISEMENTS:

and so on to the last bearings Ne/N=e

The same results will be obtained if a correction of e/N is applied to each of the observed angles. Then the first bearing will be changed by e/N the second by 2e/N, the third by 3e/N, and so on.

3. Adjustment of Closing Error:

(a) Closing Error:

While plotting a closed traverse, the end point coincides exactly with the starting point provided that work is correct. Also in a closed traverse, the algebraic sum of the latitudes- (the sum of northings-the sum of southings) should equal zero, and the algebraic sum of the departures (the sum of eastings – the sum of westings) should equal zero.

ADVERTISEMENTS:

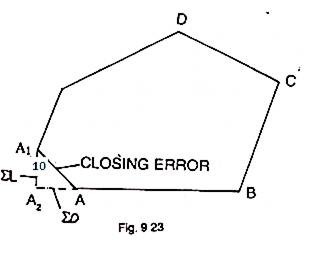
But due to errors in the field measurements of angles and distances, the traverse if plotted according to the field measurements will not close on the starting point. The distance by which the end point of a survey fails to meet with the starting one is called the closing error or error of closure. In fig. 9.23, A and A₁ are the starting and end points respectively, and AA₁ represents the closing error.

The two components of this error (A₁A₂ and AA₂) parallel and perpendicular to the meridian may be determined by finding the algebraic sum of the altitudes (ΣL), and that of the departures (ΣD). Since the triangle A₁A₂A is right angled at A₂, the linear closing error (AA₁) is equal to the square root of the sum of the squares of the algebraic sum of the latitudes and that of the departures.

i.e. closing error

= AA₁

The direction of the closing error is given by the relation.,

tan θ = where θ is the reducing bearing. The signs of ΣL and ΣD will define the quadrant of the closing error.

(b) Balancing the Traverse:

It is process of adjusting the latitudes and departures by applying corrections to them in such a way that the algebraic sum of the latitudes, and that of the departures should each equal to zero, i.e. the sum of the northings should be exactly equal to the sum of the southings, and the sum of the easting should be exactly equal to the sum of the westing.

The following rules may be used for finding the corrections to balance the survey:

(1) Bowditch’s Rule:

It is also known as the compass rule and is most commonly used in traverse adjustment. It is used when the angular and linear measurements are equally precise. By this rule, the total error in latitude and that in departure is distributed in proportion to the lengths of the sides.

Correction to latitude or departure of any side