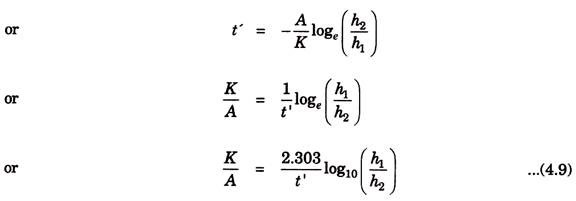How to Determine the Yield of an Open Well?: 2 Tests | Water Engineering

The yield of an open well can be found by the following two practical methods or yield tests: 1. Constant Level Pumping Test 2. Recuperation Test.

1. Constant Level Pumping Test:

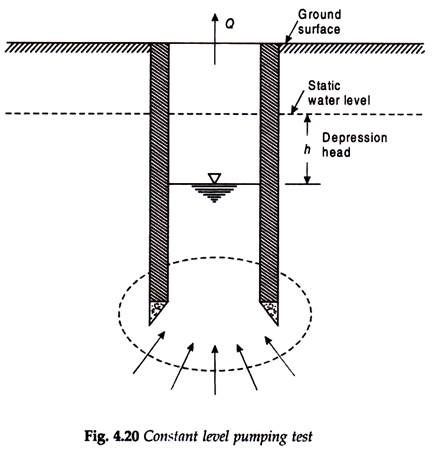
In this test water is pumped from the open well so that the water level in the well is depressed by an amount h known as depression head (or draw-down) as shown in Fig. 4.20. The rate of pumping is then so adjusted that the water level in the well remains constant. In this condition the rate of pumping will be equal to the rate of yield from the well at this depression head. The rate of pumping of water is measured by a suitable discharge measuring device.

Thus if Q is the rate of yield (or discharge) at a depression head h and A is the area of flow section through which water enters the well (which will be equal to the cross-sectional area of the bottom of the well if the lining of the well is impervious) then from Darcy’s Law-

Q = kAi

or Q = kA h/L

or Q = CAh …(4.8)

where C (= k/L) is percolation intensity coefficient. This is a constant of the formation around the well. Its value is greater for coarser soils and smaller for finer soils. The value of C may be determined if Q, A and h are known and the same may be used to determine the rate of yield from the well for any other value of the depression head by using Eq. 4.8.

Thus for a constant depression head H, the rate of yield from a well is given by Eq. 4.8 as:

Q = CAH … (4.8 a)

In case a cavity is formed at the bottom of the well then the area A is taken as (4/3) times the cross-sectional area of the bottom of the well. This is so because if no cavity is formed at the bottom of the well, then-

A = πd²/4

where d is the diameter of the well.

On the other hand if a hemispherical cavity is formed at the bottom of the well, then

A = πd²/2

Since the area of the actual cavity formed is in between these two values, the value of A may be taken as the mean of these two values. Thus

From Eq. 4.8, it is clear that the discharge increases with the depression head. However, the depression head cannot be increased beyond a certain critical value because otherwise the velocity of water percolating in the well will be excessive and the soil particles will be disturbed and dislodged. The critical value of h at which the percolation velocity is critical is known as critical depression head. Normally the depression head is kept equal to 1/3 of the critical depression head and it is known as the working depression head.

Maximum yield or critical yield of a well will therefore be obtained corresponding to the critical depression head. The yield under the working depression head is known as the maximum safe yield of a well. From the constant level pumping test described above the maximum safe yield can be determined.

2. Recuperation Test:

Though the constant pumping test gives accurate value of safe yield of an open well, it is sometimes very difficult to adjust the rate of pumping so as to maintain a constant level of water in the well. In such circumstances, a recuperation test may be adopted which is described below.

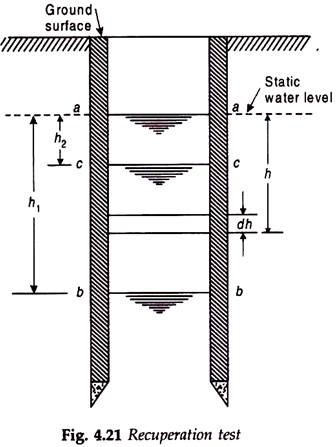
In the recuperation test water is pumped from the well so that sufficient depression head is developed. The depression head is measured and the pumping is then stopped. The water level in the well will start rising. The time taken by the water to come back to the initial static level before the pumping was started or any other measured level is then noted.

The rate of yield (or discharge) may then be determined as indicated below:

With reference to Fig. 4.21,

Let aa = static water level in the well before the pumping was started

bb = water level in the well when the pumping was stopped

h₁ = depression head in the well when the pumping was stopped

cc = water level in the well at some noted time t’ after the pumping was stopped

h₂ = depression head in the well at time t’ after the pumping was stopped

h = depression head in the well at time Rafter the pumping was stopped

dh = decrease in depression head in time dt.

Thus in time t after the pumping was stopped the water level in the well recuperated by (h₁ – h). It again recuperates by dh in a time dt after this.

∴ Volume of water entering the well when the head recuperated by dh is

dV = A dh ….(i)

where A = cross-sectional area of the well at its bottom.

Again if Q is the rate of .recharge into the well at time t under a depression head h, then the volume of water entering the well in a time dt is

Since h_1, h₂ and t’ are measured in this test, the same are known and by introducing their values in Eq. 4.9, the value of (K/A) can be calculated. (K/A) is known as the specific yield or specific capacity of an open well which is defined as the volume of water that percolates into the well per unit time per unit area under a unit depression head.

The value of K/A) is usually expressed in cubic metre per hour per square metre of area under one metre depression head. The approximate Value of (K/A) for different types of soils as indicated by Marriot are given in Table 4.2.

Knowing the value of (K/A) the rate of yield (or discharge) Q from a well under a constant depression head H may be determined as follows;

From Eq. (ii), we have

Q = KH …..(4.10)

It may however be noted that in Eq. 4.10 if time t’ is in hours then Q will be in m³ hour and if t’ is in seconds then Q will be in cumec. Further if H is the maximum depression head then the corresponding value of Q obtained from Eq. 4.10 will be the maximum yield of the well. However, if H is the average depression head, Q will the average yield of the well.